Desde meados da década de 1920 e até ao final dos anos de 1930, consolida-se a diversificação das instituições que formam Oficiais do Exército, com a reestruturação da Escola Central de Sargentos e a criação da Escola Militar de Aviação e da Escola de Serviço de Saúde Militar.

Figura 1 – Escola Central de Sargentos, em Águeda.

Encontrado no espólio bibliográfico do meu avô materno, Bento Dias Loureiro (1915-2009), e com dedicatória do próprio autor, o manual Lições de Balística, da autoria do capitão de artilharia Luiz António Vicente, professor da Escola Central de Sargentos, constitui um excelente exemplo de manual didático militar, do tempo do Estado Novo.

O objetivo deste artigo é caraterizar as Lições de Balística na Escola Central de Sargentos, na década de 1940, tendo como base o manual Lições de Balística da autoria de Luiz António Vicente, capitão de Artilharia. Este artigo vem na sequência do anteriormente publicado nesta Revista, denominado Consequências da 1ª Guerra Mundial na elaboração dos livros de Probabilidade (Revista Militar n.º 2589 – Outubro de 2017, pp. 845-854).

Como noções preliminares, define Balística Interna como o estudo do movimento dos projéteis no interior das armas e Balística Externa como o estudo do movimento dos projeteis, desde que saem da arma até atingir o alvo ou qualquer outro meio resistente.

Define trajetória como caminho percorrido pelo projétil no espaço. De entre as partes que constituem a trajetória salienta a origem, o ponto de queda, o vértice ou ponto culminante (ponto mais alto da curva), o alcance, a linha de tiro, o plano de tiro e ângulo de tiro.

Determinação da Flecha (ordenada do vértice e eixo de simetria da trajetória)

Figura 2 – Flecha.

Determinada a trajetória, tiram-se diversas cordas horizontais, marca-se o meio de cada e faz-se passar por estes pontos uma curva que irá intersetar a trajetória no ponto A e que é o vértice da curva¹. A perpendicular baixada desse ponto sobre OX será a flecha AB.

Um corpo qualquer em movimento no vácuo está unicamente sujeito a duas forças: a força da projeção e a força da gravidade. A força da projeção, que põe o projétil em movimento, é devida à expansão dos gases da pólvora. È uma força instantânea, isto é, a sua ação é exercida num tempo muito pequeno e o movimento produzido no centro de gravidade será retilíneo, uniforme e indefinido no prolongamento do eixo do cano, se nenhuma outra causa fizer variar este movimento e direção.

Analisa a influência da resistência no ar e as causas de que depende. Quanto à forma dos projeteis, defende a forma oval no sentido de minimizar a resistência do ar. Define ângulo de levantamento, de vibração ou de desvio inicial como o ângulo formado pela linha de tiro com a de projeção. Como causas que produzem o ângulo de desvio inicial apresenta o recuo das armas e as vibrações do cano. Define forçamento como sendo o conjunto de disposições que tem por fim evitar a fuga de gases da pólvora entre as paredes da boca-de-fogo e do projétil.

Define “ponto de impacto” como o centro do vestígio ou furo deixado pela bala no alvo sobre o qual faz fogo. O ponto onde a trajetória média encontra o alvo a uma dada distância denomina-se ponto médio. Como processos para a sua determinação apresenta a média das coordenadas e a mediatriz. Dá-se o nome de “desvio de um ponto de impacto em relação a um ponto ou uma linha reta” à distância desse ponto de impacto ao ponto ou à reta. Apresenta as fórmulas de cálculo do Desvio Absoluto, Desvio Absoluto Médio, Desvio Quadrático Médio. Como principais causas dos desvios dos projéteis salienta os desvios provenientes da arma, os desvios provenientes das munições e dos resíduos da pólvora do cano, os desvios provenientes do atirador e os desvios provenientes das circunstâncias exteriores.

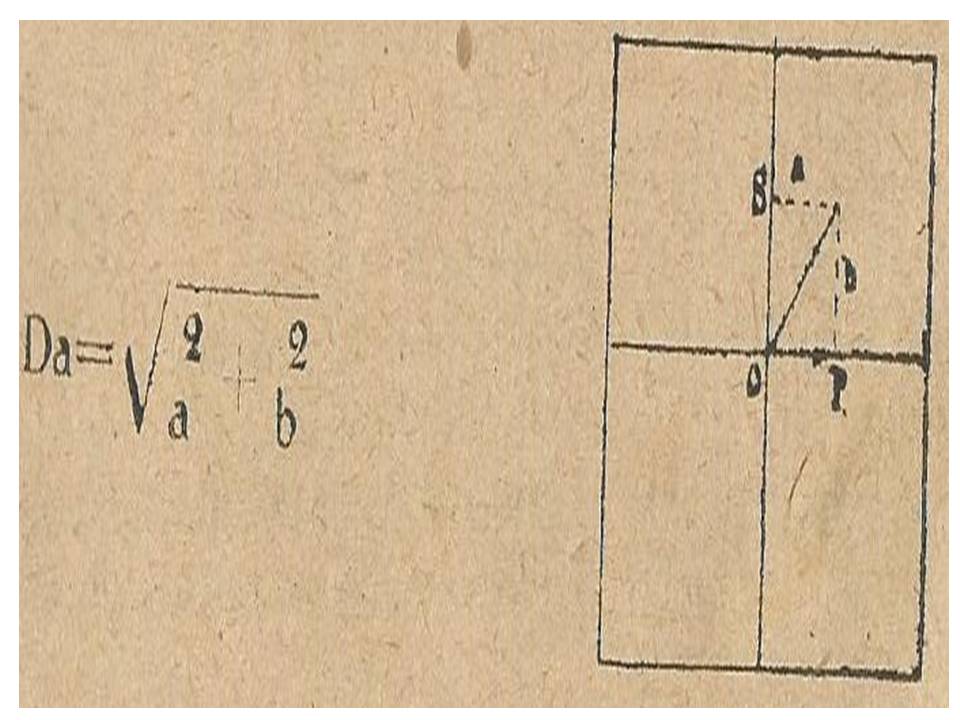
Figura 3 – Desvio absoluto.

Figura 4 – Desvio absoluto médio.

Figura 5 – Desvio quadrático médio.

Define “alça” como sendo altura variável a que se pode elevar a ranhura da mira em relação a uma determinada linha. Multiplicando o valor da “alça teórica” pelo comprimento de mira obtém-se o valor da “alça total”, que corrigida da quantidade devida ao levantamento dá a “alça real”. Explica como se determina a flecha (ordenada do vértice e eixo de simetria da trajetória) e o ângulo do tiro.

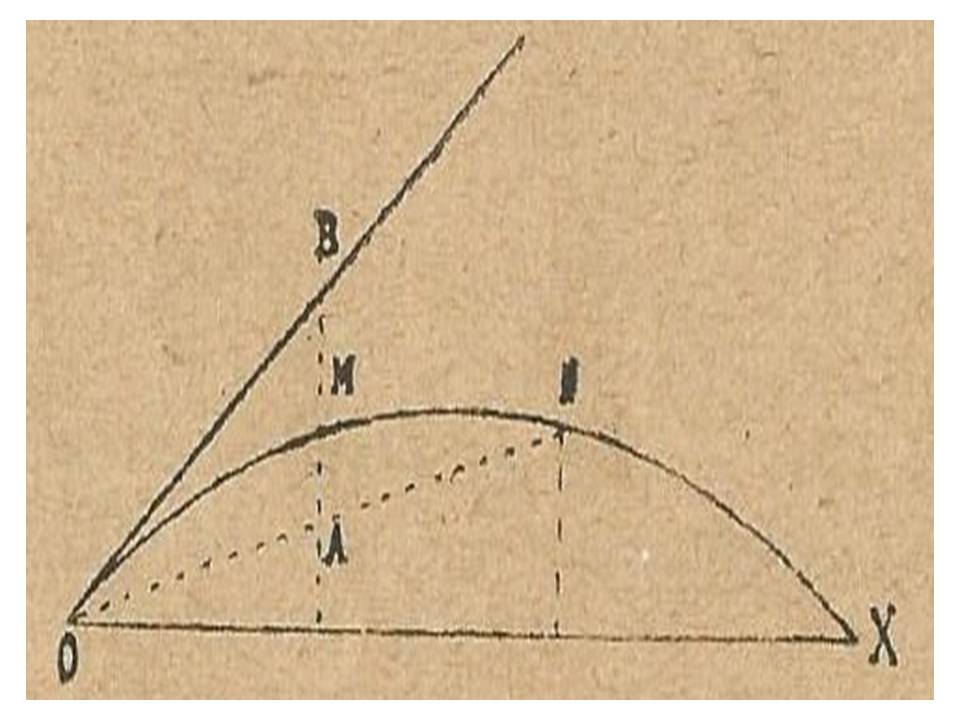
Figura 6 – Ângulo do tiro.

Para determinar graficamente o ângulo de tiro, unimos com a origem O a extremidade N de uma ordenada pouco distante. Prolonga-se depois a ordenada de um comprimento MB = MA, une-se B com O; o ângulo BOX é o ângulo do tiro.

Define Grupamento como sendo o conjunto de vestígios (pontos de impacto) deixados sobre um alvo pelos projéteis de diversos tiros, feitos da mesma posição e visando o mesmo ponto.

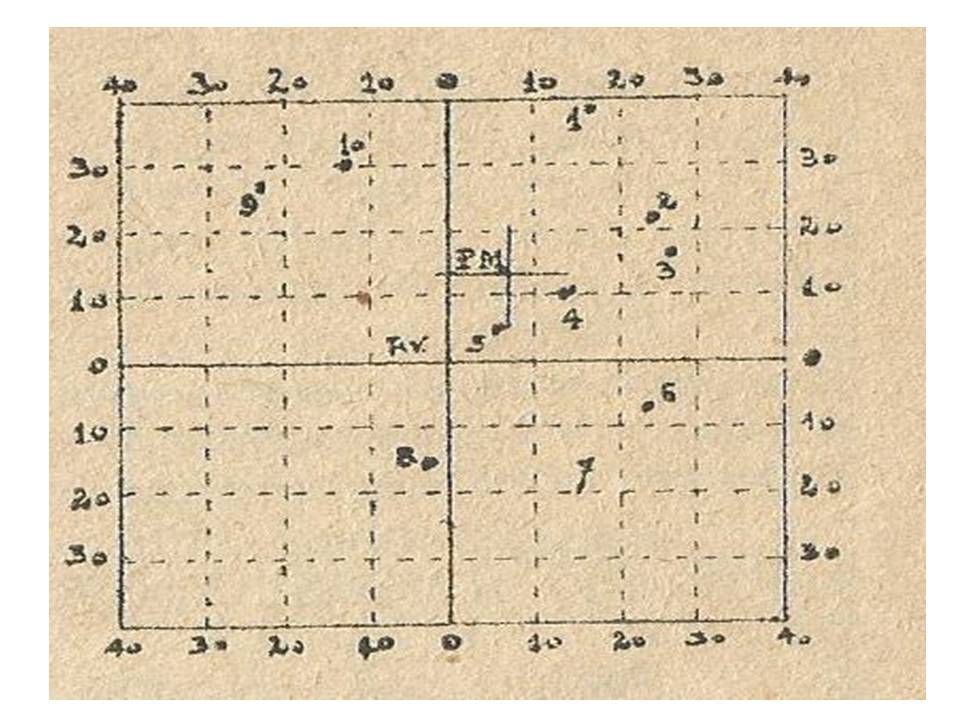
Figura 7 – Grupamento.

A noção de probabilidade de um acontecimento surge quando comparamos os casos em que ele é possível realizar-se com aqueles que são favoráveis a essa realização. Apresenta o seguinte exemplo de aplicação da noção de probabilidade: “(...) Se houvesse um número igual, seis, por exemplo, de esferas brancas e pretas, a probabilidade de tirar uma esfera branca ou preta era de 6/12; havia então tanta probabilidade de tirar uma esfera branca como uma preta”. A velocidade do tiro é expressa pelo número de tiros que um homem atira num minuto e o efeito útil é o número de balas que um atirador acerta no alvo num minuto. Define fator de probabilidade como sendo a relação entre a largura, altura ou comprimento de uma zona qualquer e a correspondente dispersão média. Apresenta tábuas de fatores de probabilidade.

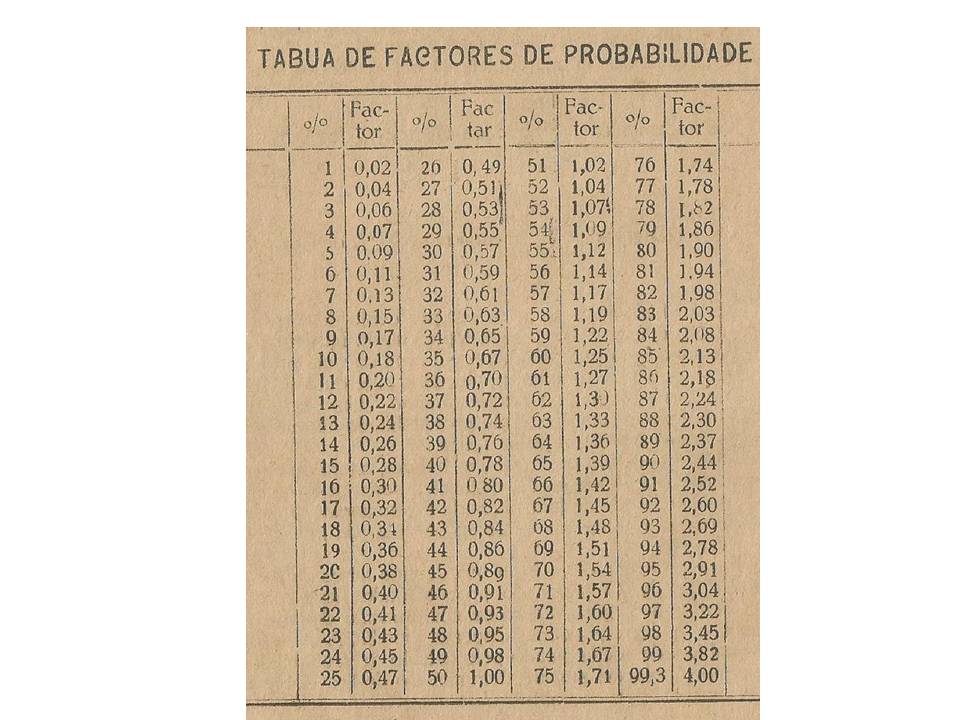
        Figura 8 – Tábua de fatores de probabilidade.

Figura 9 – Exemplo de problema utilizando a tábua de fatores de probabilidade.

Figura 10 – Exemplo de problema utilizando a tábua de fatores de probabilidade.

As curvas de justeza das armas permitem comparar a precisão de várias armas, sendo a “mais justa” aquela que tiver as ordenadas menores.

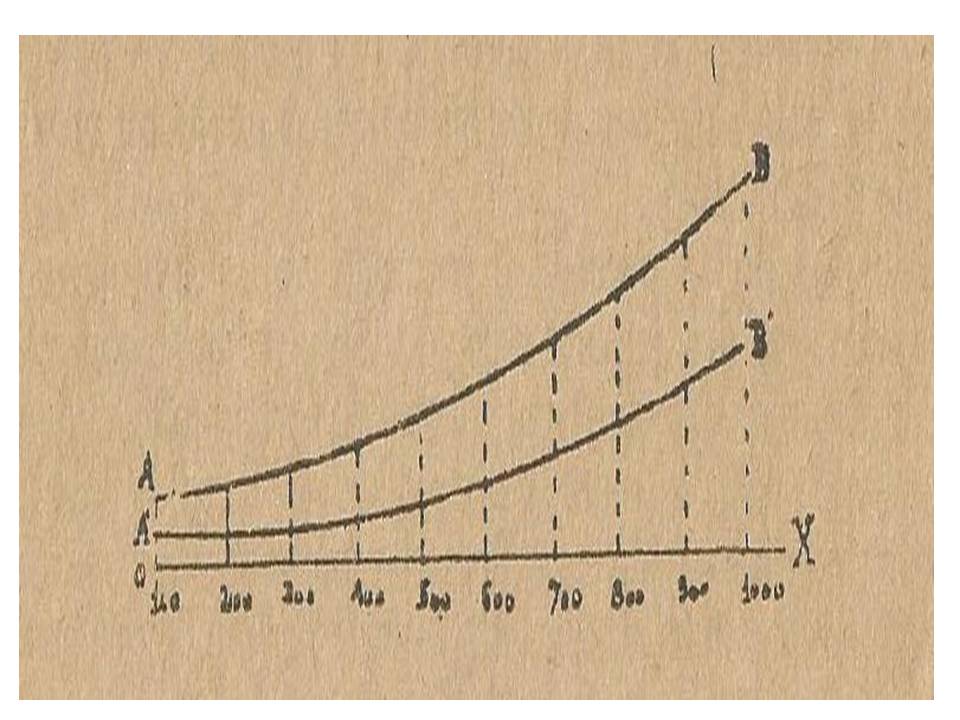
Figura 11 – Curvas de justeza das armas.

Uma trajetória é mais ou menos tensa conforme é menos ou mais elevada acima da linha de mira. Em relação a um terreno é mais ou menos rasante conforme a trajetória é mais ou menos tensa.

O tiro inclinado é definido como aquele que é executado sobre objetivos táticos situados em terrenos com inclinação superior ou inferior relativamente à linha de mira. O projétil, quando toca o terreno sob um pequeno ângulo, descreve, em geral, uma trajetória secundária à qual se dá o nome de “ricochete”.

A percentagem do tiro é expressa pelo número de balas que acertam no alvo por cada cem tiros disparados. A velocidade do tiro é expressa pelo número de tiros que um homem atira num minuto. O efeito útil é o número de balas que um atirador mete no alvo num minuto.

Define de “tiro indireto” ao tiro dirigido sobre alvos ocultos à vista do utilizador. Explica como se determina a alça do tiro indireto pelo processo das ordenadas recorrendo à semelhança de triângulos.

A carteira de tiro deverá conter a indicação dos diversos pontos de passagem provável do inimigo assim como os locais onde os atiradores da defesa deverão fazer fogo. A prancheta de tiro consiste numa carta do terreno na qual se indicam com traços ou curvas os vários pontos de queda no terreno das diferentes trajetórias, emanando do mesmo posto. O tiro mergulhante é um caso especial do tiro indireto, em que o projétil deve rasar a crista do obstáculo que se quer bater.

Se o alvo for fixo e suposta a arma carregada, para se fazer um tiro é preciso executar as seguintes operações: primeiro, graduar a alça; segundo, dar direções à arma; terceiro, tomar a linha de mira; quarto, disparar. Se o alvo for móvel, não existem regras precisas para as correções a fazer na pontaria. Se os alvos forem de elipse (aparecem e desaparecem), o atirador deve fixar atentamente a vista no ponto onde se espera que o alvo apareça.

Para terminar, tece considerações sobre a vulnerabilidade das formações sob a ação dos fogos de artilharia, a vulnerabilidade provável de uma formação e sobre a tática, apresentando tabelas.

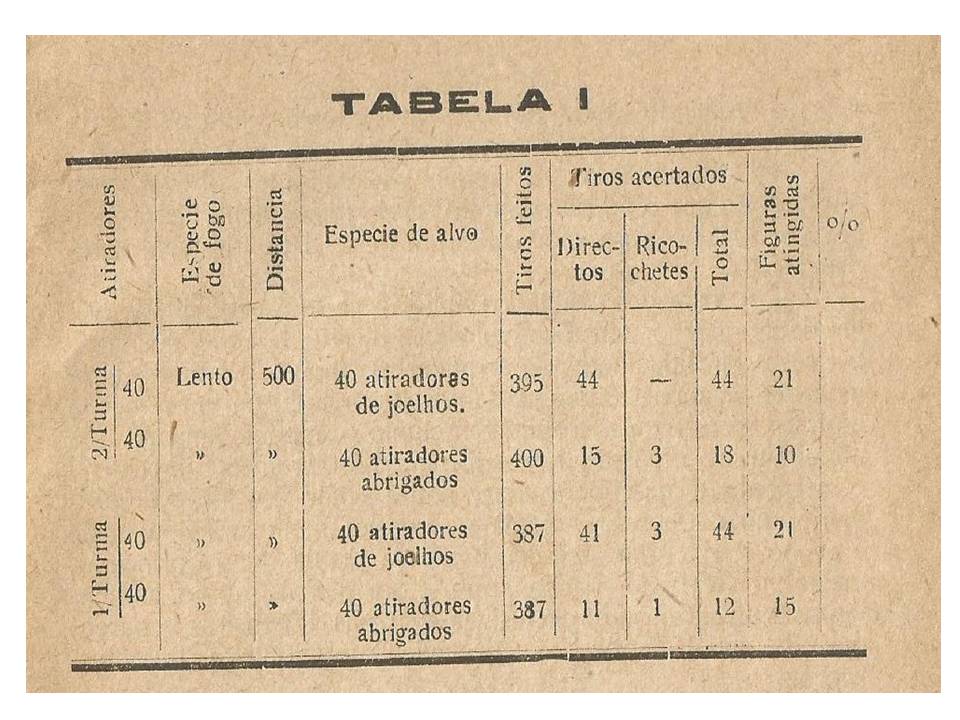
Figura 12 – Exemplo de tabela.

Afirma, citando o coronel Tafin, no seu livro “Les tirs de combate”: a vulnerabilidade do homem de joelhos está para a do homem abrigado na proporção de 3 para 2.

O manual Lições de Balística, da autoria do capitão de artilharia Luís António Vicente constitui um interessante elo de ligação entre o conhecimento militar e o conhecimento Físico e Matemático, permitindo ao leitor a familiarização de conceitos Matemáticos como Desvio Absoluto, Desvio Absoluto Médio, Desvio Quadrático Médio, Probabilidade de um Acontecimento, Semelhança de Triângulos, embora sem a profundidade de outros manuais analisados. A finalidade do autor, ao contrário de outras obras, não será a de constituir teoria, mas, sim, a de explicar conceitos fundamentais da Balística, tendo como base um conjunto de conhecimentos de Matemática e de Física.

Bibliografia

Vicente, L. (1943). Lições de Balística. Lisboa: Tipografia e Papelaria America.

Papança, F. (2011). A Matemática, a Estatística e o Ensino nos Estabelecimentos de Formação de Oficiais do Exército Português no Período 1837-1926: Uma Caracterização. S. Mamede de Infesta: Edium Editores.

Papança, F. (2017). Consequências da 1ª Guerra Mundial na elaboração dos livros de Probabilidade. Revista Militar nº 2589 – Outubro de 2017, pp. 845-854.

Aubert, J. (1919). La probabilité dans les tirs de guerre. Paris: Gauthier Villars.

Burilano, S. (1911). Probabilité du Tir. Paris: Octave Doin et Fils, Éditeurs.

Haag, J. (1926). Applications au Tir. Em Émilie Borel (Ed.), Traité du Calcul des Probabilites (Tomo IV). Paris: Gauthier Villars.

Gonçalves, N. (1909). 6ª cadeira-Introdução ao estudo dos projecteis-Probabilidades do Tiro. Lisboa: Tip. da Escola do Exército.

Sena, C. (1925). Elementos de Balística. Lisboa: Litografia da Escola Militar.

Cunha, E. (1940). O Professor José Nunes Gonçalves e a sua Obra (Resumo). Em Discursos e Comunicações apresentadas ao Congresso da História da Actividade Científica Portuguesa (VIII Congresso), 12º Vol., Tomo 1º, 1ª secção. Lisboa: Congresso do Mundo Português Publicações.

Gonçalves, N. (1894). Theoria do movimento de rotação dos projecteis oblongos. Lisboa: Escola do Exército.

Gonçalves, N. (1895). 6ª cadeira-Introdução ao estudo dos projecteis-Probabilidades do Tiro. Lisboa: Escola do Exército.

Gonçalves, N. (1895). 6ª cadeira-Introdução ao estudo dos projecteis-Probabilidades do Tiro. Lisboa: Typ. da Academia Real das Sciencias de Lisboa.

Gonçalves, N. (1900). Provas mecânicas dos aços para canhões. Lisboa: Typ. La Bécarre de Francisco J. Carneiro.

Gonçalves, N. (1903). Estudo do movimento dos projecteis na alma das boccas de fogo. Lisboa: Typ. da Academia Real das Sciencias de Lisboa.

Gonçalves, N. (1929). Balística Interna. Lisboa: Imprensa Nacional.

Gonçalves, N. (1932). Balística Externa. Lisboa: Imprensa Nacional.

Gonçalves, N. (1938). Balística Aplicada: lições professadas na 6ª cadeira da extinta Escola do Exército, no ano lectivo de 1901-1902. Lisboa: Imprensa Nacional.

Sena, C. & Gonçalves, N. (1923). Balística Interna. Lisboa: Litografia da Escola Militar.

Sena, C. (1919). Estudo sôbre o emprego da pólvora sem fumo no carregamento das bôcas de fogo em serviço que ainda usam póvora negra. Lisboa: Escola de Guerra.

Barreiros, J. (1845). Instrução theorico-pratica sobre artilharia. Lisboa: Escola do Exército.

_______________________________

¹ Poder-se-á conjeturar que o autor entende a noção de reta simplesmente como um conjunto de pontos, querendo dizer que a curva interseta cada uma das cordas.