1. Introdução
Segundo Artur Bívar, no seu Dicionário Geral e Analógico da Língua Portuguesa, Medir é relacionar grandezas, comparando uma grandeza variável com outra constante, chamada Unidade de Medida. Como unidades de medida foram inicialmente utilizadas relações com o homem e suas dimensões.
O passo, o palmo, o pé, o cúbito e a polegada.
Os egípcios usaram o “cubitus”, distância que ia do cotovelo às pontas dos dedos esticados, e que correspondia a 52,4 cm. Posteriormente os gregos usaram o “digitus” ou dedo, correspondendo a 19,3 mm, a qual deu origem à actual polegada.
Após a Revolução Francesa, as unidades de medida passaram a relacionar-se com as dimensões do planeta Terra, onde se dizia que um metro era a décima milionésima parte do quarto do meridiano terrestre, pelo que o meridiano mediria cerca de 40.000 km.
Actualmente e desde 1983, essa relação passou a ser relacionada com a velocidade da luz, ou seja um metro é a distância percorrida pela luz em (1/ 299.792.458) do segundo de tempo.
2. Investigações
Para dar uma noção da tremenda confusão que reinava em Portugal, antes de ser assinada a Convenção do Metro, em 20 de Maio de 1875, já fez 133 anos, passarei a resumir algumas das unidades de medição existentes na época. Estamos no reinado de D. Luís e Filipe Folque morre no ano anterior.
Vasculhando alguns alfarrábios encontrei um estudo elaborado por Gastão de Matos, à data capitão prestando serviço na Repartição de Geodesia do Instituto Geográfico e Cadastral, de Lisboa. Tal estudo tinha então sido pedido por alguém da Argentina, que se encontrava fazendo “un trabajo de ordenamiento y classificacion de mapas e cartas geográficas”.
Começa o autor por referir a origem da palavra Légua, termo já conhecido no séc. IV depois de Cristo, como Leuca em latim e utilizada por Ammiano Marcelino1 historiador em Roma.
Na Península Ibérica, a primeira referência a Leucas é da responsabilidade de Santo Isidoro de Sevilha,2 frade estudioso e Bispo de Sevilha, que viveu entre os séculos VI e VII, também depois de Cristo.
O astrónomo árabe Almamum3 (780-850) conseguiu medir o comprimento do grau terrestre numa planície e obteve para essa distância “duzentos mil e quinhentos côvados” (±136.340 metros).
O Rei Afonso X de Castela (1252-1284), mais conhecido como “o Sábio”, também incentivou o estudo da Astronomia o que por certo ajudou na medição do grau do meridiano.
Para valor da Légua pensava-se ser equivalente a 1.500 passos romanos, mas mais tarde a Légua francesa teria mais de 2.000 passos. Pelo pensamento de Santo Ildefonso4 (Bispo de 657 a 667) a mesma Légua mas medida em Toledo teria 5.000 passos, o que nas medidas actuais corresponderia a uma distância entre 7.200 a 8.200 metros.
Entretanto com as variações dos passos duplos e dos geométricos veio a fixar-se aproximadamente a extensão da Légua nas nações mediterrânicas, desde um pouco acima de 4.000 metros até um pouco abaixo dos 6.000 metros. Para os germânicos a légua tinha 7.500 metros.
De acordo com os dados informados por Iraci del Nero da Costa5 (Pesos e Medidas no período colonial brasileiro: denominações e relações, FEA, USP), e admitindo-se que a "polegada" em questão era equivalente a 2,75 centímetros, pode-se construir a seguinte relação:
1 légua = 3.000 braças = 6.000 varas = 30.000 palmos = 240.000 polegadas = 660.000 centímetros = 6.600 metros
Em Portugal, durante o período de transição das antigas unidades de medida para o sistema métrico, por Decreto de 2 de Maio de 1855, foi estabelecida a légua métrica, equivalente a 5.000 metros.
Na época das navegações, existiu um outro tipo de légua, a légua marítima. Seu cálculo diferia de navegador para navegador pois era feito com base em duas medidas:
- do perímetro da terra que, por volta do século XVI, era considerado ser cerca de 40.000 km; e
- da quantidade de léguas que cada navegador considerava que possuía cada grau do meridiano terrestre.
Se um navegador considerasse que cada um dos 360 graus possuísse 18,5 léguas, cada légua marítima possuiria 6.006,00 metros. Devido a essas variações, a medida da légua era expressa de várias formas:
- Légua de 18 ao grau, equivalente a 6.172,4 metros
- Légua de 20 ao grau, equivalente a 5.555,56 metros (medida oficial da légua marítima)
- Légua de 25 ao grau, equivalente a 4.444,44 metros
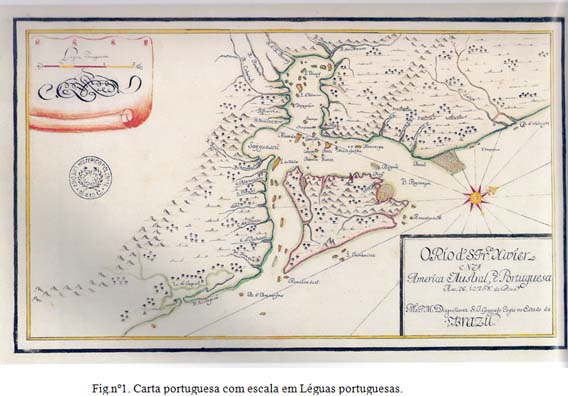
Entretanto Alexandre Zorzi,6 em 1503, numa carta que abrange a América do Sul, escreveu ao longo da costa uma observação indicando:
“Terra desconhecida. Terra vista pelos portugueses a sul a 600 Léguas. Chama-se Brazil”.
Em Portugal foram também usadas como medidas de comprimento:
Passos no séc.X d.C. e Estádios no séc. XIII d.C.
Segundo Fontoura da Costa7, o mais antigo texto português em que figura a légua, como medida itinerária, está no Cancioneiro da Ajuda8 (1270/1350) e como medida marítima nos escritos de Azurara (séc. XV d.C.) 9.
Como vimos entre os séculos XVI e XVIII d.C., a légua era de extensão muito variável. “Teoricamente era um múltiplo de certa unidade base, mas apesar dos esforços de vários soberanos, principalmente do Rei D. Sebastião, não foi possível estabelecer craveira certa para essa unidade em todo o Reino”.
Depois da Idade Média e em Portugal parece terem sido usadas:
- Légua comum portuguesa;
- Légua do Ribatejo;
- Légua marítima ou Espanhola;
- Légua usada nas medidas agrárias no Brasil.
A ideia base era de que uma légua corresponderia aproximadamente ao caminho percorrido por um homem caminhando a pé durante uma hora de tempo.
No entanto e teoricamente, o comprimento das léguas seria sempre uma fracção do círculo máximo, mas como a terra está longe de ser esférica e a precisão das medições era não só pequena mas também muito variável, os seus valores flutuavam ao sabor das interpretações pessoais dos estudiosos.
As navegações eram feitas com rumos e distâncias, muito sujeitas a erros.
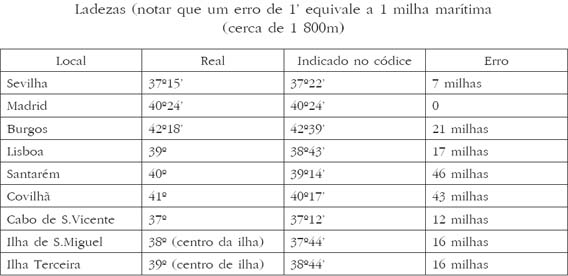
Na biblioteca de Évora pode ver-se um códice que trata experimentalmente dos erros das cartas resultantes desse tipo de avaliações, onde Duarte Pacheco10 apresenta latitudes (ladezas), para diferentes pontos da Terra tendo sido escolhidos os referentes a Portugal e Espanha.
Duarte Pacheco, a partir destes dados, atribuiu ao grau o comprimento de 18 léguas, mas tal dimensão vai contra a maioria dos navegadores portugueses da época, que atribuíam ao grau o valor de 17,5 léguas. Estas diferenças, segundo Fontoura Costa, complicaram a interpretação das cláusulas do Tratado de Tordezilhas, na Junta de Badajoz em 1524, pelo que não se chegou a acordo nenhum.
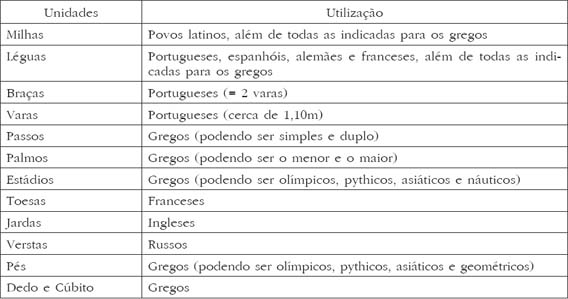
Em Cartografia Terrestre, aparecem as mais variadas unidades sendo as mais vulgares indicadas em:
Perante esta trapalhada de unidades, foi muito difícil relacionar todas estas medidas.
- os italianos com Cadamosto11,(Navegador, 1432 a 1488) relacionaram 1 légua com 4 milhas e assim o considerou Cristóvão Colombo;
- o milanês Leonardo Torriani12 (Engenheiro Militar italiano) relacionou 7 léguas com 25 milhas (1 légua = 3,750 milhas);
- pouco depois Manuel de Figueiredo diz que a légua vale “três milhas, pouco mais”;
- autores árabes atribuíam ao grau o valor de 16 léguas e 1/3, opinião também de Pedro Nunes13 (1502 a 1578) e de Francisco Faleiro14, português que trabalhou em Sevilha em 1535.
- era no entanto o valor de 17,5 léguas ao grau que a maioria dos nautas portugueses utilizava.
O Padre Simão Falónio15 que ensinava matemática no colégios dos jesuítas de Santo Antão entre 1635 e 1642, dizia que este comprimento de grau teria sido obtido por experiência, mas não se sabe de quem. Os seus livros estiveram na Biblioteca Nacional de Lisboa, e suponho que parte ainda estarão.
Já no séc. XVII um discípulo de Falónio sintetizava para os seus alunos, as unidades de medida conhecidas:
Como disse, neste Colégio de S. Antão funcionava a Aula de esfera, onde na era filipina se estudaram as defesas de Portugal e das Colónias baseadas em praças-fortes. O Colégio de S. Antão foi considerado a mais importante instituição de ensino científico desde finais do séc. XVI a meados do séc. XVIII, em Portugal.
No capítulo VI da Geometria Elementar em uso nesse curso, eram referidos alguns instrumentos usados para as medições em “planemetria”: A figura nº 5 apresenta a “cadeia de argolinhas” mais conhecida por Cadeia do Agrimensor. Era definida como:
Hua cadea de arame, dividida por humas argolinhas de dez em dez palmos ou pés.Os lados se medirão no papel por hua linha dividida em partes iguais a que chamão Escala ou Petipé, a qual representa o mesmo género de medidas que forão tomadas no terreno, como por exemplo palmos, pés ou braças.
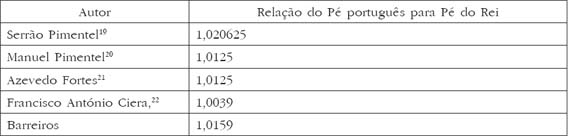
Serrão Pimentel16, em 1673 ainda ensinava que o grau teria 17,5 léguas. E em 1717, o jesuíta António Cordeiro17 informa, na sua obra “História Insulana das terras a Portugal Sugeitas…”, que as distâncias entre as ilhas dos Açores eram medidas em léguas.
Podemos dizer que as unidades base dos sistemas de medidas lineares português e castelhano deviam ser respectivamente o palmo e o pé. Autores mais tardios, notam que a légua portuguesa e a castelhana são iguais, mas diferentes as varas, sendo a castelhana mais curta.
Entretanto foram aparecendo mais unidades, como:
- o palmo craveiro de Lisboa;
- o côvado dos mercadores, mais ou menos equivalente a três palmos, sendo diferente do côvado ou cubitus usado nas obras de matemática.
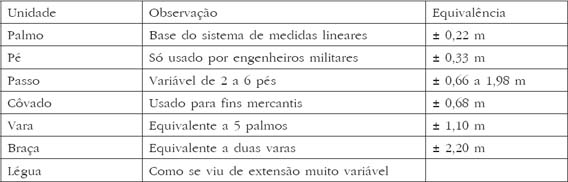
Podemos analisar algumas equivalências na época:
1 pé = 1,5 palmos
1 vara = 5 palmos
1 vara curta = 4 palmos
1 braça = 10 palmos
1 braça marítima = 8 palmos
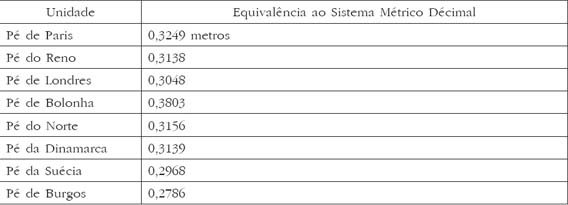
No livro “Mesurer la Terre” de Levallois18, pode ler-se que as medidas variavam de estado para estado, de província para província e de vila para vila. Para valor do comprimento dos “pés” poderemos ter uma equivalência a medidas actuais:
Filipe Folque23 fala-nos também da Braça Ciera, a qual nos dava para o Palmo português o valor de 0,2193 m.
Quando Ciera iniciou as medições de campo, recorreu a todas as repartições públicas para obter o padrão exacto da braça portuguesa de 10 palmos. Dada a incerteza e a variedade que encontrou, resolveu compor uma medida, a que chamou Braça Ciera (1 braça = 2,1980 metros) que estivesse em razão finita com alguma conhecida na Europa, tendo utilizado a Toesa da Academia Real das Ciências de Lisboa e considerado 25 toesas equivalentes a 22 braças. A toesa padrão, existente na Academia, foi feita em Londres, aferida pela da Academia das Ciências de Paris e remetida para Lisboa em 1787.24
Mas há mais unidades como:
- o pé da Ribeira das Naus
- o palmo de Côvado
- o palmo da Junta de Comércio
- a braça Marítima.
Todavia, apesar da grande influência de Azevedo Fortes e posteriormente de Francisco António Ciera, os cartógrafos portugueses continuaram, pelo menos até ao fim do século XVIII a empregar indiferentemente a légua de 20 ao grau, de 18 ao grau e principalmente de 17,5 ao grau.
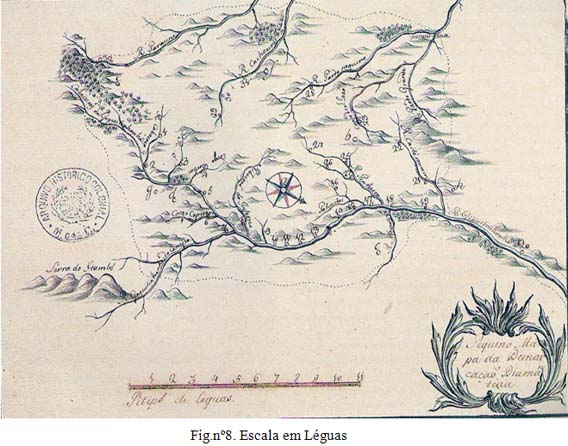
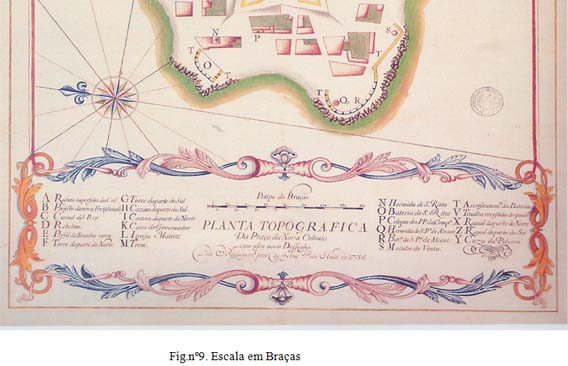
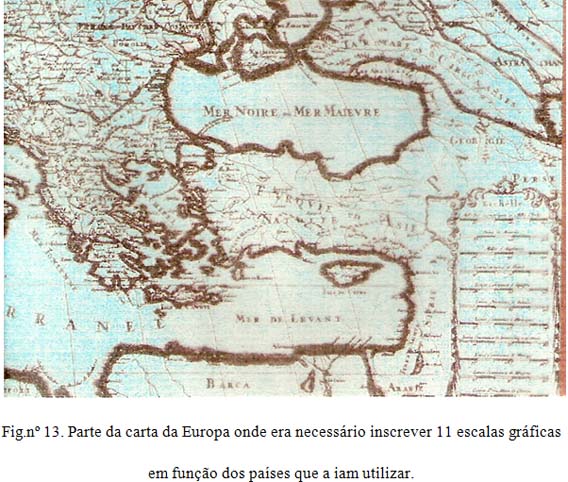
Da revista Oceanus com vários números publicados, quando das comemorações dos Descobrimentos portugueses 1999/2000, em 29 cartas e mapas, as respectivas escalas ou petipé, onze foram medidas em léguas, sete em palmos, sete em braças, duas em pés, uma em passos outra em varas.
Trata-se principalmente de cartografia dos séculos XVII e XVIII, cobrindo o tema, o Achamento do Brasil.
A ligação da dimensão terrestre do grau de meridiano, como se sabe, já vem dos árabes e mesmo de Eratóstones25, pois ele é que determinou o perímetro terrestre, com maior aproximação no séc. II a.C. No entanto como medições mais rigorosas tiveram lugar as de Snellius26, já com triangulação geodésica, o qual mediu um arco de 1º11’30” entre Alkmar e Gerg-op-Zoan no sentido Norte-Sul e obteve 55.100 toesas ao grau.
Tempos depois Picard e outros geodestas, como os das expedições científicas à Lapónia e ao Peru, onde foram obtidos outros valores, como a seguir se indicam:
Posteriormente Mechain e Delambre medem o arco entre Dunkerque e Barcelona e concluíram que:
- Um quarto do meridiano tem 5.130.740 toesas o que indica que:
- O Meridiano terá 20.522.960 toesas.
Se o Meridiano equivale a 40.000 quilómetros, um metro terá:
0,513074 toesas
E uma toesa terá:
1.949.036.591 metros.
Foi portanto mais fácil dividir o Meridiano em 40.000.000 metros do que em 20.522.960 toesas.
É provável que perto do ano de 1745 se tivesse conhecimento dos resultados obtidos pelas duas expedições, mas como a da Lapónia durou só dois anos e a do Peru perto de 10 anos, e ainda porque como os resultados diferiam uns dos outros, os seus autores não se entendiam, e ainda por se terem agravado as relações entre a Espanha e a França, os resultados finais não condiziam e não se pretendia difundi-los. Penso que as missões portuguesas de delimitação fronteiriça, enviadas ao Brasil entre 1750 e 1778, teriam também por finalidade calcular o comprimento do grau do meridiano, mas não se sabe quais as conclusões a que chegaram ou mesmo se chegaram a alguma.
Em 1720 o Conselho Ultramarino indicava ao Rei de Portugal que:
“Embora o governador de S.Paulo tivesse nomeado um jesuíta para fazer os mapas do sertão, não era de esperar que nem esse religioso nem o engenheiro da capitania tivessem os conhecimentos necessários para fazer o mapa com o rigor exigido, uma vez que necessitava da sciencia particular da cosmographia, para poder arrumar as terras, os rios e os montes, pelos graus.”
Seguiram então para o Brasil em 1730, o jesuíta português Diogo Soares27 e o italiano Domingos Capassi, este último com superiores conhecimentos de astronomia e dedicado ao cálculo de coordenadas geográficas, mas como se disse, nada constou depois.
Na obra “Tesouros da Cartografia Portuguesa” editada em 1997, a medida mais vulgar nas cartas é a légua, embora em plantas parcelares se usem os palmos. Há ainda equivalências entre léguas portuguesas e japonesas e as milhas italianas: Para agudizar o problema, há mais informações sobre
No livro “A caminho da Índia” editado em 1964, podem ver-se outras equivalências:
Em Castela a unidade mais usual era a vara cuja equivalência se fazia à toesa. Assim,
3. O país que finalmente conseguiu unificar toda esta trapalhada, foi a França
Em França a medida pé (le pied) foi usada durante cerca de 1.000 anos, e a sua origem estava ligada ao tamanho do Pé Real de Carlos Magno. No entanto após a Revolução Francesa, houve necessidade de ser criada uma medida dentro do sistema decimal, que fosse de fácil tratamento e com boa aceitação pelos outros países. Funciona já há cerca de 200 anos e não tem sido contestada, embora os anglófonos ainda reclamem.
Denis Guedj28, no seu livro “A Meridiana” obra romanceada sobre a criação do metro em França, em plena Revolução, relata os dissabores dos geómetras Jean B. Delambre29 e Pierre Méchin30, quando foram incumbidos pela Assembleia Legislativa de estabelecer uma medida universal para medição de distâncias. Com a queda do Absolutismo, seria muito difícil manter uma centralização que não chocasse os cidadãos. Por meio desta unificação dos sistemas de medida (e pesos) foi conseguido o controlo dos cidadãos principalmente à distância. A liberdade das diversas regiões tinha como consequência o enfraquecimento do poder central. Só a unificação dos sistemas de medidas e dos pesos, poderia permitir manter e mesmo aumentar os impostos, sem que o povo notasse. Tais medidas foram elaboradas e accionadas por quem sabia e não por populares, mesmo em França, país da igualdade, etc..
Antes da Convenção do Metro, em 1875, as medidas em França eram principalmente:
A toesa | para medir objectos |
O pé real | para medir distâncias no terreno |
Essas unidades tinham as seguintes relações:
Ainda depois da Convenção do Metro, em 1888 na Astronomia Popular de Flammarion31, as distâncias celestes são indicadas em milhões de Léguas. Porquê? Será por inércia?
Na busca de um estalão de medida universal, para as expedições à Lapónia e ao Peru foi escolhida a toesa de Chatelet. Depois das expedições esta mudou de nome, passando a ser conhecida pela toesa do Peru. Esta toesa era uma medida arbitrária, de uma distância existente num muro do Chatelet de Paris, entre duas extremidades de uma régua de ferro.
Face às alterações revolucionárias introduzidas a toesa não resistiu mais tempo, e criado o Metro, este foi relacionado como sendo:
443,295936 linhas da Toesa do Peru.
Entre 1816 e 1831 os geómetras F. G. Struve32 e Tenner33 conseguiram medir o arco do meridiano entre o Cabo Norte (Noruega) e o Mar Negro (Rússia). Struve obteve para o grau do meridiano o valor de 57.144 toesas (11.375,747m) depois de juntar os seus cálculos com os de Tenner, o qual fez a parte sul do trajecto, quase todo na Rússia de então. No entanto é de atender que cada geodeta usava um talão de medida diferente.
Struve usou a toesa do Peru, com 1.728 linhas de comprimento.
Tenner usou um talão de medida chamado “séjane russe” de difícil tradução, com 945 linhas de comprimento.
A medida de comprimento “o pé”, não foi usado porque havia discrepâncias entre essas unidades:
1 pé francês = aproximadamente = 1,067 Pés ingleses.
Julgamos que esta pequena diferença não se compara com a diferença entre as unidades usadas por Struve e Tenner, mas enfim que sabemos nós? Estes trabalhos permitiram, já no séc. XX a ligação à Cidade do Cabo. E falando desta cidade, também aí tinha sido medido o grau do meridiano pelo Abade La Caille em 1752, tendo sido obtido para o Grau o valor de 57.037 toesas,ou seja 111.167,20001metros.
Apesar da internacionalização do Metro e das suas relações com as medidas anglo-saxónicas, os problemas têm-se mantido e durante a 2ª Grande Guerra as peças acessórias fabricadas nos EUA não serviam nos instrumentos fabricados pelos ingleses, porque se descobriu então que a polegada americana tinha 0,0254005 m e que a inglesa tinha 0,02539993 m.
Segundo Claude Million34, o Metro foi imposto pelo Imperialismo Geodésico. Segundo o mesmo autor a grande vantagem do metro é a sua divisão decimal, como aliás também aconteceu com a introdução dos grados centesimais (gones).
Mas também havia outro tipo de unidades para medir distâncias, como a hora de marcha.
4. Conclusões
I - Em França, foi preciso unificar (os pesos e medidas) para governar, pelo que a unificação das medidas será antidemocrática!
II - Das dezenas de medidas utilizadas, foram mais usadas em Portugal:
III - As relações entre estas unidades, sempre difíceis de estipular, foram-no em França, após a sua revolução, mas não imediatamente.
IV - Durante anos ainda funcionaram outras unidades fora do sistema decimal, mas na comunidade científica só as nações anglo-saxónicas, ainda mantém as suas anacrónicas unidades, pelo que se pode agradecer à Revolução Francesa essa unificação e normalização quase a nível mundial.
V - Assim podemos concluir que:
A Légua da Póvoa, noção de distância muito antiga, entranhada no povo português, distância essa de definição indeterminada, mantém a sua posição e valor ao longo de muitos anos, continuando perfeitamente indefinida.
_______________
* Tenente-Coronel de Artilharia.
________________
1 Historiador Romano do fim do império, (325/391).
2 Doutor da Igreja, 560/636.
3 Califa árabe, governou até 833.
4 Santo visigótico.
5 Economista Brasileiro.
6 Cartógrafo italiano.
7 Oficial de marinha de Guerra, professor da Escola Naval e da Náutica.
8 Primeiras manifestações da literatura portuguesa, desde o séc.XII d.C.
9 Guarda conservador da Livraria Real em 1451.
10 Duarte P. Pereira, (1460/1533) navegador, militar, geógrafo. Assinou o Tratado de Tordesilhas e reconheceu a costa brasileira antes de Cabral (?).
11 Terá descoberto algumas ilhas de Cabo Verde.
12 Engenheiro e Arquitecto italiano, às ordens de D. Filipe II, fortificou as Ilhas Canárias, o Forte do Bugio, S. Julião da Barra e na Cidade de Salvador (séc.XVI).
13 Matemático português.
14 Cosmógrafo português que trabalhou com Fernão de Magalhães desde 1517.
15 Leccionou Astronomia na Aula de Esfera, foi engenheiro mor do reino em 1641.
16 Tenente-General de Artilharia, Cosmógrafo e Engenheiro Mor entre 1641 e 1671.
17 A. Cordeiro viveu de 1640 a 1722, e ensinou no Colégio de S. Antão. Nasceu em Angra.
18 Publicação da Association des Geométres Experts - França.
19 Tenente-General de Artilharia, autor do “Método Lusitano de Desenhar Fortificações de Praças regulares e irregulares” 1680.
20 Filho de Serrão Pimentel, autor da Arte de Navegar de 1699.
21 Manoel Azevedo Fortes, Eng.º. Militar; professor de matemática na Academia Militar de Fortificação em 1895. Publicou entre outros “o Engenheiro Português”.
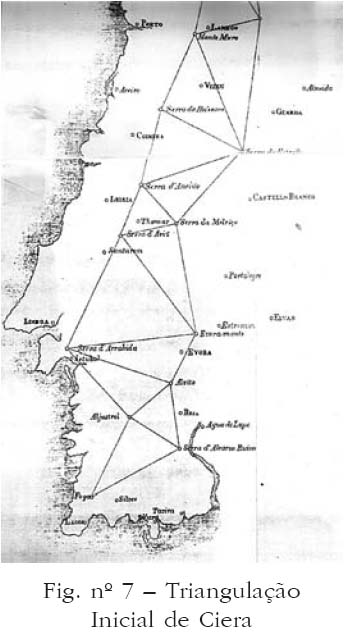
22 Francisco António Ciera, pai da Triangulação Geral do Reino, para fins cartográficos (1763/1814).
23 General, lente da Escola Politécnica de Lisboa, construtor da Carta Geral do Reino na escala 1/100.000.
24 Maria Helena Dias - www.instituto - camoes.pt/cvc/ciência/p48.html.
25 Filósofo de Alexandria, (276-196 a.C.) estimou o valor do raio da Terra.
26 Geodeta holandês, (1580-1626) desenvolveu a triangulação geodésica.
27 Com Domingos Capassi foram em 1729 para Brasil, sendo os primeiros astrónomos e matemáticos a cartografar sistematicamente o Brasil com Latitudes e Longitudes. Ref.ª Clóvis Pereira da Silva, em A Matemática no Brasil.
28 Professor de História da Ciência na Universidade de Paris.
29 Astrónomo francês (1749/1822).
30 Astrónomo e Topógrafo francês (1744/1804).
31 Astrónomo francês, e criador de obras populares sobre astronomia. (1842/1925).
32 Astrónomo estónio (1793/1864).
33 Astrónomo lituano (1783/1859).
34 Autor do livro La Topographie, Presses Universitaires, 1957.